Двоичное число: прямой, обратный и дополнительный коды

Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Прямой, обратный и дополнительный коды двоичного числа - способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.

---

Прямой код

Прямой код - способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел

Прямой код используется в двух вариантах.
В первом (основной) - для записи только неотрицательных чисел:

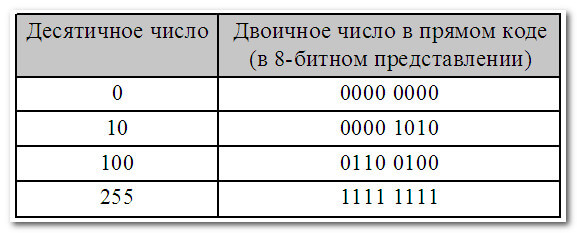В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 - от 0 до 255)

Второй вариант - для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае - восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
- знаковый разряд равен 0, то число положительное
- знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от - 127 до +127:

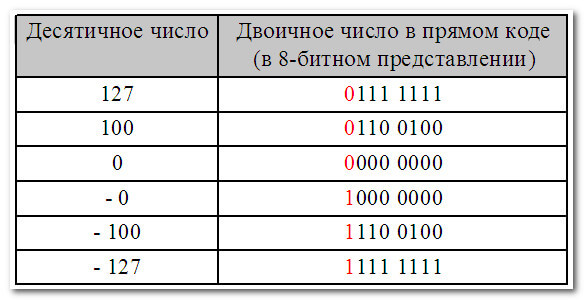Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Прямой код используется главным образом для представления неотрицательных чисел.
 Использование прямого кода для представления отрицательных чисел является неэффективным - очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля - положительный ноль и отрицательный ноль (чего не бывает):

---

Обратный код

Обратный код - метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) - двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) - двоичной цифры 1, за которым следует инвертированное значение положительного числа.

Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.

При 8-битном двоичном числе - знаковый бит (как и в прямом коде) старший (8-й)

Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127

Арифметические операции с отрицательными числами в обратном коде:

(Арифметические операции с двоичными числами)

1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = - 0001 1001
Необходимо их сложить:
100 + (-25) = 100 - 25 = 75

1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0001 1001
-25= 1110 0110
и складываем два числа:
0110 0100 (100) + 1110 0110 (-25) = 1 0100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд - переполнение), = 0100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0100 1010 + 1 = 0100 1011 (знаковый бит =0, значит число положительное), что равно 75 в десятичной системе

2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = - 0000 1010
Необходимо их сложить:
5 + (-10) = 5 - 10 = -5

1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0000 1010
-10= 1111 0101
и складываем два числа:
0000 0101 (5) + 1111 0101 (-10) = 1111 1010 (знаковый бит =1, значит число отрицательное)

2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1111 1010 ----> 1000 0101
Проверяем:
1000 0101 = - 0000 0101 = -5

---

Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
- арифметические операции проводятся в два этапа
- как и в прямом коде два представления нуля - положительный и отрицательный

---

Дополнительный код

Дополнительный код - наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.

В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).

Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
- инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
- к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0000 1010 ----> -10 = 1000 1010
Инвертируем значение (получаем обратный код):
1000 1010 ----> 1111 0101
К полученной инверсии прибавляем 1:
1111 0101 + 1 = 1111 0110 - десятичное число -10 в дополнительном коде

2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0000 1010
Вычитаем из нуля:
0 - 0000 1010 = 1111 0110 - десятичное число -10 в дополнительном коде

Арифметические операции с отрицательными числами в дополнительном коде

Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде

Как мы видим на этом примере - дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.

---

Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода

---

Предыдущие статьи:
1. Микроконтроллеры - первый шаг
2. Системы счисления: десятичная, двоичная и шестнадцатиричная
3. Логические операции, логические выражения, логические элементы
4. Битовые операции

---

(44 голосов, оценка: 4,68 из 5)

Загрузка...

---