Обработка данных движения какого-либо объекта – весьма востребованная в современном мире технология, широко применяющаяся при создании различных роботов, самоуправляемых автомобилей, дронов и многого другого. Для полноценной обработки данных движения объекта необходимо взаимодействовать с такими параметрами как линейное ускорение, угловое ускорение и магнитный север (magnetic north).

Ранее на нашем сайте мы уже рассматривали подключение к плате Arduino датчика акселерометра и гироскопа MPU6050 и магнитометра HMC5883L. Но MPU9250 является более универсальным датчиком – он объединяет в себе возможности гироскопа, акселерометра и магнитометра. И в данной статье мы рассмотрим его подключение к плате Arduino и обработку получаемых с него данных (калибровку, автокалибровку, фильтрацию и усреднение).
Необходимые компоненты
- Плата Arduino Mega 2560 (купить на AliExpress) (можно также использовать и другие типы плат Arduino).
- Датчик MPU9250 (купить на AliExpress).
Общие сведения о датчике MPU9250
Датчик MPU9250 реализует функции 3-осевого гироскопа, 3-осевого акселерометра и 3-осевого магнитометра, то есть он представляет собой 9-ти осевой IMU сенсор (Inertial Measurement Unit – инерционное измерительное устройство). Его внешний вид с распиновкой контактов показан на следующем рисунке.

Назначение контактов датчика MPU9250:
| Обозначение контакта | Назначение контакта |
| VCC | Внешнее питание 3.3 В |
| GND | Общий |
| SCL | Линия тактовых импульсов I2C и SPI |
| SDA | Линия данных для I2C или SPI |
| EDA | Линия данных при подключении внешних датчиков по шине I2C |
| ECL | Линия тактов при подключении внешних датчиков по шине I2C |
| AD0 | Для выставления адреса I2C в режиме I2C. В режиме SPI это линия данных от датчика |
| INT | Линия прерываний. Срабатывание настраивается при конфигурировании датчика MPU-9250 |
| NCS | В режиме SPI – линия выбора ведомого (chip select). В режиме I2C не соединяется ни с чем |
| FSYNC | Зависит от конфигурации |
MPU9250 является самым миниатюрным в мире девятиосевым датчиком. Это говорит о высокой производительности его микросхемы. Состоит корпус датчика из двух мельчайших кристаллов, один из которых отвечает за гироскоп и акселерометр, а другой за магнитометр. Данные с них обрабатываются встроенным сигнальным процессором DMP с помощью алгоритмов Motion Fusion и передаются по интерфейсам I2C или SPI.
Рассмотрим более подробно работу составных частей датчика.
Гироскоп – это сенсор, реагирующий на изменение углов ориентации в пространстве.
Акселерометр сравнивает проекцию ускорения объекта с гравитационным ускорением и способен замерять линейную скорость объекта, а вкупе с гироскопом – и положение в пространстве.
Магнитометр представляет собой устройство для измерения интенсивности ближайшего магнитного поля, действующего на объект.
Датчик MPU9250 позволяет измерять такие параметры как угол yaw (рыскание), угол pitch (тангаж) и угол roll (крен). Графическое изображение этих параметров представлено на следующем рисунке.

Схема проекта
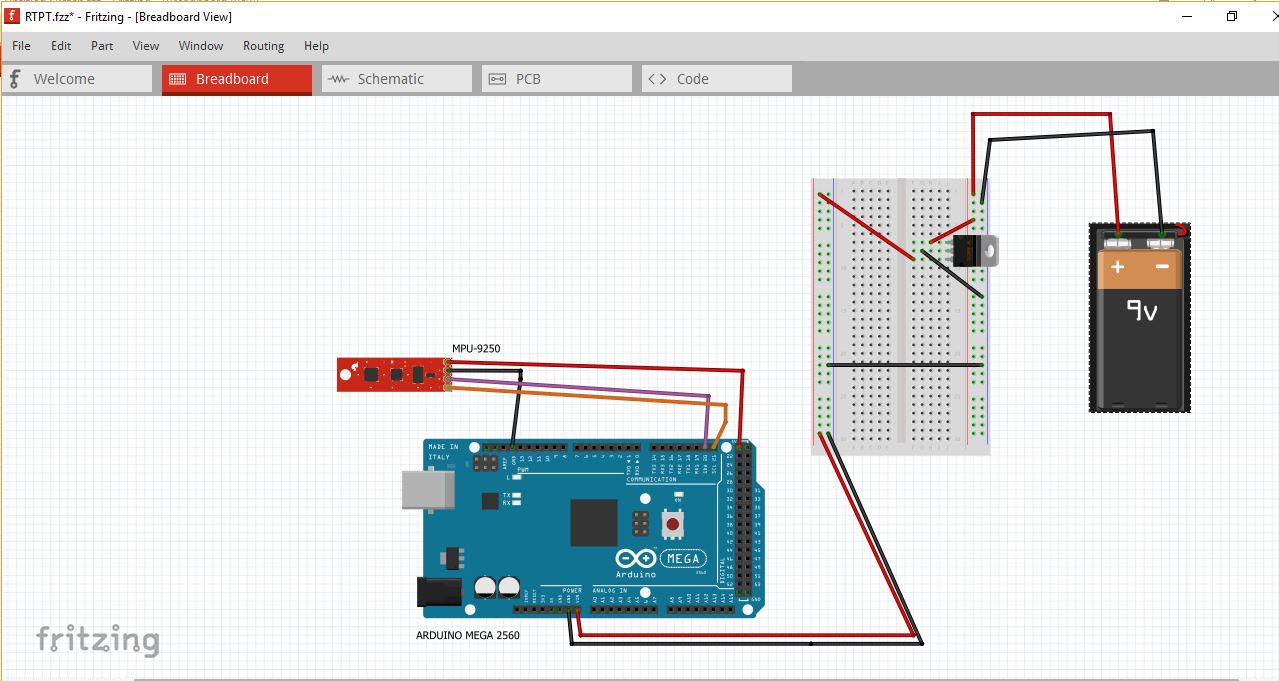
Схема подключения датчика MPU9250 к плате Arduino представлена на следующем рисунке.
Подключать датчик MPU9250 к плате Arduino можно по интерфейсу I2C или интерфейсу SPI. В нашем случае мы использовали подключение по интерфейсу I2C (5V, Gnd, SCL, SDA). При использовании интерфейса SPI необходимо будет задействовать 5 контактов на плате модуля (5V, Gnd, SCL, SDA, CS, SDO).
Питать модуль можно как от напряжения от 5 В, поскольку на плате датчика имеется линейный стабилизатор для данного типа питания, так и от напряжения 3,3 В.
Обработка данных от датчика MPU9250
MPU9250 имеет 16-битный регистр для каждого из 3-х датчиков, входящих в его состав. Они временно хранят данные от датчика прежде чем произойдет их передача по интерфейсу I2C.
Считывание данных
Для взаимодействия с датчиком MPU9250 мы будем использовать библиотеку, разработанную пользователем kriswiner. Скачать ее можно по адресу – https://github.com/kriswiner/MPU9250.
Мы будем считывать данные по 8 бит и затем объединять их в 16-битные. Это реализуется следующим фрагментом кода из библиотеки kriswiner’а:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
fifo_count = ((uint16_t)data[0] << 8) | data[1]; packet_count = fifo_count/12;// How many sets of full gyro and accelerometer data for averaging for (ii = 0; ii < packet_count; ii++) { int16_t accel_temp[3] = {0, 0, 0}, gyro_temp[3] = {0, 0, 0}; readBytes(MPU9250_ADDRESS, FIFO_R_W, 12, &data[0]); // read data for averaging accel_temp[0] = (int16_t) (((int16_t)data[0] << 8) | data[1] ) ; // Form signed 16-bit integer for each sample in FIFO accel_temp[1] = (int16_t) (((int16_t)data[2] << 8) | data[3] ) ; accel_temp[2] = (int16_t) (((int16_t)data[4] << 8) | data[5] ) ; gyro_temp[0] = (int16_t) (((int16_t)data[6] << 8) | data[7] ) ; gyro_temp[1] = (int16_t) (((int16_t)data[8] << 8) | data[9] ) ; gyro_temp[2] = (int16_t) (((int16_t)data[10] << 8) | data[11]) ; accel_bias[0] += (int32_t) accel_temp[0]; // Sum individual signed 16-bit biases to get accumulated signed 32-bit biases accel_bias[1] += (int32_t) accel_temp[1]; accel_bias[2] += (int32_t) accel_temp[2]; gyro_bias[0] += (int32_t) gyro_temp[0]; gyro_bias[1] += (int32_t) gyro_temp[1]; gyro_bias[2] += (int32_t) gyro_temp[2]; } |
Калибровка исходных/необработанных данных (Raw Data)
Получаемые с датчика MPU9250 данные должны быть откалиброваны в соответствии с оборудованием пользователя, в котором будет использоваться датчик. Калибровка магнитометра требуется для компенсации магнитного склонения (Magnetic Declination). Корректировочное значение в данном случае сильно зависит от местоположения датчика. Необходимо откалибровать две переменные: yaw и magbias.
Ниже приведенный фрагмент кода реализует калибровку переменной yaw для магнитного склонения, характерного для местности: Potheri, Chennai, India.
Данные о магнитном склонении в конкретной местности можно получить, к примеру, с помощью следующих сайтов:
- http://geomag.nrcan.gc.ca/calc/mdcal-en.php;
- http://www.ngdc.noaa.gov/geomag-web/.
|
1 2 3 4 5 6 7 8 9 10 |
yaw = atan2(2.0f * (q[1] * q[2] + q[0] * q[3]), q[0] * q[0] + q[1] * q[1] – q[2] * q[2] – q[3] * q[3]); pitch = -asin(2.0f * (q[1] * q[3] – q[0] * q[2])); roll = atan2(2.0f * (q[0] * q[1] + q[2] * q[3]), q[0] * q[0] – q[1] * q[1] – q[2] * q[2] + q[3] * q[3]); pitch *= 180.0f / PI; yaw *= 180.0f / PI; yaw += 1.34; /* Declination at Potheri, Chennail ,India Model Used: IGRF12 Help Latitude: 12.823640° N Longitude: 80.043518° E Date Declination 2016-04-09 1.34° W changing by 0.06° E per year (+ve for west )*/ |
В следующем фрагменте кода реализована калибровка переменной magbias, которая взята из функции magcalMPU9250(float * dest1, float * dest2) (из библиотеки, которую мы используем для работы с датчиком MPU9250).
|
1 2 3 4 5 6 7 8 9 10 11 |
readMagData(magCount); // Read the x/y/z adc values getMres(); // magbias[0] = +470.; // User environmental x-axis correction in milliGauss, should be automatically calculated // magbias[1] = +120.; // User environmental x-axis correction in milliGauss // magbias[2] = +125.; // User environmental x-axis correction in milliGauss // Calculate the magnetometer values in milliGauss // Include factory calibration per data sheet and user environmental corrections mx = (float)magCount[0]*mRes*magCalibration[0] – magBias[0]; // get actual magnetometer value, this depends on scale being set my = (float)magCount[1]*mRes*magCalibration[1] – magBias[1]; mz = (float)magCount[2]*mRes*magCalibration[2] – magBias[2]; } |
Автоматическая калибровка магнитометра
Это одна из самых простых, но в то же время важных участков кода программы. Функция magcalMPU9250(float * dest1, float * dest2) производит калибровку магнитометра в то время когда вы перемещаете его по фигуре восьмерки (цифры “8”). Она сохраняет максимальные и минимальные значения, а затем на их основе вычисляет среднее.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
void magcalMPU9250(float * dest1, float * dest2) { uint16_t ii = 0, sample_count = 0; int32_t mag_bias[3] = {0, 0, 0}, mag_scale[3] = {0, 0, 0}; int16_t mag_max[3] = {0x8000, 0x8000, 0x8000}, mag_min[3] = {0x7FFF, 0x7FFF, 0x7FFF}, mag_temp[3] = {0, 0, 0}; Serial.println(“Mag Calibration: Wave device in a figure eight until done!”); sample_count = 128; for(ii = 0; ii < sample_count; ii++) { readMagData(mag_temp); // Read the mag data for (int jj = 0; jj < 3; jj++) { if(mag_temp[jj] > mag_max[jj]) mag_max[jj] = mag_temp[jj]; if(mag_temp[jj] < mag_min[jj]) mag_min[jj] = mag_temp[jj]; } delay(135); // at 8 Hz ODR, new mag data is available every 125 ms } // Get hard iron correction mag_bias[0] = (mag_max[0] + mag_min[0])/2; // get average x mag bias in counts mag_bias[1] = (mag_max[1] + mag_min[1])/2; // get average y mag bias in counts mag_bias[2] = (mag_max[2] + mag_min[2])/2; // get average z mag bias in counts dest1[0] = (float) mag_bias[0]*mRes*magCalibration[0]; // save mag biases in G for main program dest1[1] = (float) mag_bias[1]*mRes*magCalibration[1]; dest1[2] = (float) mag_bias[2]*mRes*magCalibration[2]; // Get soft iron correction estimate mag_scale[0] = (mag_max[0] – mag_min[0])/2; // get average x axis max chord length in counts mag_scale[1] = (mag_max[1] – mag_min[1])/2; // get average y axis max chord length in counts mag_scale[2] = (mag_max[2] – mag_min[2])/2; // get average z axis max chord length in counts float avg_rad = mag_scale[0] + mag_scale[1] + mag_scale[2]; avg_rad /= 3.0; dest2[0] = avg_rad/((float)mag_scale[0]); dest2[1] = avg_rad/((float)mag_scale[1]); dest2[2] = avg_rad/((float)mag_scale[2]); Serial.println(“Mag Calibration done!”); } |
Для более детального изучения данного вопроса рекомендуем обратиться к источнику: https://github.com/kriswiner/MPU6050/wiki/Simple-and-Effective-Magnetometer-Calibration.
Постоянная калибровка для определенного места
Если вы не хотите каждый раз при включении устройства производить автоматическую калибровку магнитометра, то вы должны записать средние значения переменной magbias[] после их вычислений с помощью следующего фрагмента кода:
|
1 2 3 4 5 6 7 8 9 10 |
readMagData(magCount); // Read the x/y/z adc values getMres(); magbias[0] = +470.; // User environmental x-axis correction in milliGauss, should be automatically calculated magbias[1] = +120.; // User environmental x-axis correction in milliGauss magbias[2] = +125.; // User environmental x-axis correction in milliGauss // Calculate the magnetometer values in milliGauss // Include factory calibration per data sheet and user environmental corrections mx = (float)magCount[0]*mRes*magCalibration[0] – magBias[0]; // get actual magnetometer value, this depends on scale being set my = (float)magCount[1]*mRes*magCalibration[1] – magBias[1]; mz = (float)magCount[2]*mRes*magCalibration[2] – magBias[2]; } |
Значения 470, 120, 125 фиксированы для местоположения автора проекта, поэтому после выполнения данной процедуры нет необходимости вызова функции void magcalMPU9250(float * dest1, float * dest2), поэтому вы можете закомментировать или удалить ее из программы. Также не забудьте закомментарить в программе ее вызов как сделано в следующем примере кода:
|
1 2 3 4 5 6 7 8 9 10 11 |
delay(1000); // Get magnetometer calibration from AK8963 ROM initAK8963(magCalibration); Serial.println(“AK8963 initialized for active data mode….”); // Initialize device for active mode read of magnetometer getMres(); //magcalMPU9250(magBias,magScale); // commented call statement if(SerialDebug) { // Serial.println(“Calibration values: “); Serial.print(“X-Axis sensitivity adjustment value “); Serial.println(magCalibration[0], 2); Serial.print(“Y-Axis sensitivity adjustment value “); Serial.println(magCalibration[1], 2); Serial.print(“Z-Axis sensitivity adjustment value “); Serial.println(magCalibration[2], 2); } |
Фильтрация данных
Поскольку исходные данные (raw data) содержат достаточно большое количество шума, мы будем использовать различные фильтры (Madgwick/Mahony/Kalman) чтобы преобразовать их в кватернионы (Quaternions).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 |
void MadgwickQuaternionUpdate(float ax, float ay, float az, float gx, float gy, float gz, float mx, float my, float mz) { float q1 = q[0], q2 = q[1], q3 = q[2], q4 = q[3]; // short name local variable for readability float norm; float hx, hy, _2bx, _2bz; float s1, s2, s3, s4; float qDot1, qDot2, qDot3, qDot4; // Auxiliary variables to avoid repeated arithmetic float _2q1mx; float _2q1my; float _2q1mz; float _2q2mx; float _4bx; float _4bz; float _2q1 = 2.0f * q1; float _2q2 = 2.0f * q2; float _2q3 = 2.0f * q3; float _2q4 = 2.0f * q4; float _2q1q3 = 2.0f * q1 * q3; float _2q3q4 = 2.0f * q3 * q4; float q1q1 = q1 * q1; float q1q2 = q1 * q2; float q1q3 = q1 * q3; float q1q4 = q1 * q4; float q2q2 = q2 * q2; float q2q3 = q2 * q3; float q2q4 = q2 * q4; float q3q3 = q3 * q3; float q3q4 = q3 * q4; float q4q4 = q4 * q4; // Normalise accelerometer measurement norm = sqrt(ax * ax + ay * ay + az * az); if (norm == 0.0f) return; // handle NaN norm = 1.0f/norm; ax *= norm; ay *= norm; az *= norm; // Normalise magnetometer measurement norm = sqrt(mx * mx + my * my + mz * mz); if (norm == 0.0f) return; // handle NaN norm = 1.0f/norm; mx *= norm; my *= norm; mz *= norm; // Reference direction of Earth’s magnetic field _2q1mx = 2.0f * q1 * mx; _2q1my = 2.0f * q1 * my; _2q1mz = 2.0f * q1 * mz; _2q2mx = 2.0f * q2 * mx; hx = mx * q1q1 – _2q1my * q4 + _2q1mz * q3 + mx * q2q2 + _2q2 * my * q3 + _2q2 * mz * q4 – mx * q3q3 – mx * q4q4; hy = _2q1mx * q4 + my * q1q1 – _2q1mz * q2 + _2q2mx * q3 – my * q2q2 + my * q3q3 + _2q3 * mz * q4 – my * q4q4; _2bx = sqrt(hx * hx + hy * hy); _2bz = -_2q1mx * q3 + _2q1my * q2 + mz * q1q1 + _2q2mx * q4 – mz * q2q2 + _2q3 * my * q4 – mz * q3q3 + mz * q4q4; _4bx = 2.0f * _2bx; _4bz = 2.0f * _2bz; // Gradient decent algorithm corrective step s1 = -_2q3 * (2.0f * q2q4 – _2q1q3 – ax) + _2q2 * (2.0f * q1q2 + _2q3q4 – ay) – _2bz * q3 * (_2bx * (0.5f – q3q3 – q4q4) + _2bz * (q2q4 – q1q3) – mx) + (-_2bx * q4 + _2bz * q2) * (_2bx * (q2q3 – q1q4) + _2bz * (q1q2 + q3q4) – my) + _2bx * q3 * (_2bx * (q1q3 + q2q4) + _2bz * (0.5f – q2q2 – q3q3) – mz); s2 = _2q4 * (2.0f * q2q4 – _2q1q3 – ax) + _2q1 * (2.0f * q1q2 + _2q3q4 – ay) – 4.0f * q2 * (1.0f – 2.0f * q2q2 – 2.0f * q3q3 – az) + _2bz * q4 * (_2bx * (0.5f – q3q3 – q4q4) + _2bz * (q2q4 – q1q3) – mx) + (_2bx * q3 + _2bz * q1) * (_2bx * (q2q3 – q1q4) + _2bz * (q1q2 + q3q4) – my) + (_2bx * q4 – _4bz * q2) * (_2bx * (q1q3 + q2q4) + _2bz * (0.5f – q2q2 – q3q3) – mz); s3 = -_2q1 * (2.0f * q2q4 – _2q1q3 – ax) + _2q4 * (2.0f * q1q2 + _2q3q4 – ay) – 4.0f * q3 * (1.0f – 2.0f * q2q2 – 2.0f * q3q3 – az) + (-_4bx * q3 – _2bz * q1) * (_2bx * (0.5f – q3q3 – q4q4) + _2bz * (q2q4 – q1q3) – mx) + (_2bx * q2 + _2bz * q4) * (_2bx * (q2q3 – q1q4) + _2bz * (q1q2 + q3q4) – my) + (_2bx * q1 – _4bz * q3) * (_2bx * (q1q3 + q2q4) + _2bz * (0.5f – q2q2 – q3q3) – mz); s4 = _2q2 * (2.0f * q2q4 – _2q1q3 – ax) + _2q3 * (2.0f * q1q2 + _2q3q4 – ay) + (-_4bx * q4 + _2bz * q2) * (_2bx * (0.5f – q3q3 – q4q4) + _2bz * (q2q4 – q1q3) – mx) + (-_2bx * q1 + _2bz * q3) * (_2bx * (q2q3 – q1q4) + _2bz * (q1q2 + q3q4) – my) + _2bx * q2 * (_2bx * (q1q3 + q2q4) + _2bz * (0.5f – q2q2 – q3q3) – mz); norm = sqrt(s1 * s1 + s2 * s2 + s3 * s3 + s4 * s4); // normalise step magnitude norm = 1.0f/norm; s1 *= norm; s2 *= norm; s3 *= norm; s4 *= norm; // Compute rate of change of quaternion qDot1 = 0.5f * (-q2 * gx – q3 * gy – q4 * gz) – beta * s1; qDot2 = 0.5f * (q1 * gx + q3 * gz – q4 * gy) – beta * s2; qDot3 = 0.5f * (q1 * gy – q2 * gz + q4 * gx) – beta * s3; qDot4 = 0.5f * (q1 * gz + q2 * gy – q3 * gx) – beta * s4; // Integrate to yield quaternion q1 += qDot1 * deltat; q2 += qDot2 * deltat; q3 += qDot3 * deltat; q4 += qDot4 * deltat; norm = sqrt(q1 * q1 + q2 * q2 + q3 * q3 + q4 * q4); // normalise quaternion norm = 1.0f/norm; q[0] = q1 * norm; q[1] = q2 * norm; q[2] = q3 * norm; q[3] = q4 * norm; } // Similar to Madgwick scheme but uses proportional and integral filtering on the error between estimated reference vectors and // measured ones. void MahonyQuaternionUpdate(float ax, float ay, float az, float gx, float gy, float gz, float mx, float my, float mz) { float q1 = q[0], q2 = q[1], q3 = q[2], q4 = q[3]; // short name local variable for readability float norm; float hx, hy, bx, bz; float vx, vy, vz, wx, wy, wz; float ex, ey, ez; float pa, pb, pc; // Auxiliary variables to avoid repeated arithmetic float q1q1 = q1 * q1; float q1q2 = q1 * q2; float q1q3 = q1 * q3; float q1q4 = q1 * q4; float q2q2 = q2 * q2; float q2q3 = q2 * q3; float q2q4 = q2 * q4; float q3q3 = q3 * q3; float q3q4 = q3 * q4; float q4q4 = q4 * q4; // Normalise accelerometer measurement norm = sqrt(ax * ax + ay * ay + az * az); if (norm == 0.0f) return; // handle NaN norm = 1.0f / norm; // use reciprocal for division ax *= norm; ay *= norm; az *= norm; // Normalise magnetometer measurement norm = sqrt(mx * mx + my * my + mz * mz); if (norm == 0.0f) return; // handle NaN norm = 1.0f / norm; // use reciprocal for division mx *= norm; my *= norm; mz *= norm; // Reference direction of Earth’s magnetic field hx = 2.0f * mx * (0.5f – q3q3 – q4q4) + 2.0f * my * (q2q3 – q1q4) + 2.0f * mz * (q2q4 + q1q3); hy = 2.0f * mx * (q2q3 + q1q4) + 2.0f * my * (0.5f – q2q2 – q4q4) + 2.0f * mz * (q3q4 – q1q2); bx = sqrt((hx * hx) + (hy * hy)); bz = 2.0f * mx * (q2q4 – q1q3) + 2.0f * my * (q3q4 + q1q2) + 2.0f * mz * (0.5f – q2q2 – q3q3); // Estimated direction of gravity and magnetic field vx = 2.0f * (q2q4 – q1q3); vy = 2.0f * (q1q2 + q3q4); vz = q1q1 – q2q2 – q3q3 + q4q4; wx = 2.0f * bx * (0.5f – q3q3 – q4q4) + 2.0f * bz * (q2q4 – q1q3); wy = 2.0f * bx * (q2q3 – q1q4) + 2.0f * bz * (q1q2 + q3q4); wz = 2.0f * bx * (q1q3 + q2q4) + 2.0f * bz * (0.5f – q2q2 – q3q3); // Error is cross product between estimated direction and measured direction of gravity ex = (ay * vz – az * vy) + (my * wz – mz * wy); ey = (az * vx – ax * vz) + (mz * wx – mx * wz); ez = (ax * vy – ay * vx) + (mx * wy – my * wx); if (Ki > 0.0f) { eInt[0] += ex; // accumulate integral error eInt[1] += ey; eInt[2] += ez; } else { eInt[0] = 0.0f; // prevent integral wind up eInt[1] = 0.0f; eInt[2] = 0.0f; } // Apply feedback terms gx = gx + Kp * ex + Ki * eInt[0]; gy = gy + Kp * ey + Ki * eInt[1]; gz = gz + Kp * ez + Ki * eInt[2]; // Integrate rate of change of quaternion pa = q2; pb = q3; pc = q4; q1 = q1 + (-q2 * gx – q3 * gy – q4 * gz) * (0.5f * deltat); q2 = pa + (q1 * gx + pb * gz – pc * gy) * (0.5f * deltat); q3 = pb + (q1 * gy – pa * gz + pc * gx) * (0.5f * deltat); q4 = pc + (q1 * gz + pa * gy – pb * gx) * (0.5f * deltat); // Normalise quaternion norm = sqrt(q1 * q1 + q2 * q2 + q3 * q3 + q4 * q4); norm = 1.0f / norm; q[0] = q1 * norm; q[1] = q2 * norm; q[2] = q3 * norm; q[3] = q4 * norm; } |
Усреднение данных
Поскольку данные на выходе датчика изменяются очень быстро, мы будем производить их выборку в течение определенного промежутка времени (50 ms) и вычислять их среднее значение.
|
1 2 3 4 5 6 7 8 9 |
count = millis(); digitalWrite(myLed, !digitalRead(myLed)); // toggle led } } else { // Serial print and/or display at 0.5 s rate independent of data rates delt_t = millis() – count; if (delt_t > 50) { // update once per half-second independent of read rate if(SerialDebug) { |
Получение “реальных” значений
Наконец, на завершающем этапе обработки данных, мы получим значения параметров yaw, pitch и roll из кватернионов.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
yaw = atan2(2.0f * (q[1] * q[2] + q[0] * q[3]), q[0] * q[0] + q[1] * q[1] – q[2] * q[2] – q[3] * q[3]); pitch = -asin(2.0f * (q[1] * q[3] – q[0] * q[2])); roll = atan2(2.0f * (q[0] * q[1] + q[2] * q[3]), q[0] * q[0] – q[1] * q[1] – q[2] * q[2] + q[3] * q[3]); pitch *= 180.0f / PI; yaw *= 180.0f / PI; yaw += 1.34; /* Declination at Potheri, Chennail ,India Model Used: IGRF12 Help Latitude: 12.823640° N Longitude: 80.043518° E Date Declination 2016-04-09 1.34° W changing by 0.06° E per year (+ve for west )*/ roll *= 180.0f / PI; Serial.print(“Yaw, Pitch, Roll: “); Serial.print(yaw+180, 2); Serial.print(“, “); Serial.print(pitch, 2); Serial.print(“, “); Serial.println(roll, 2); |
Считывание данных с датчика MPU9250 в плату Arduino Mega 2560
Для работы с датчиком MPU9250 существует достаточно много библиотек, но мы будем использовать одну из самых популярных среди них: MPU-9250 Arduino Library by Kriswiner.
Когда вы сохраните библиотеку в ваш каталог Arduino, можно приступать к работе с ней. Откройте пример MPU9250BasicAHRS.ino.
Также выполните следующие соединения в схеме:
MPU9250 Breakout ——— Arduino
• VIN ———————- 5V
• SDA ———————– SDA (Pin 20)
• SCL ———————– SCL (Pin 21)
• GND ———————- GND
Помните о том, что соединительные провода в нашем случае не должны быть очень длинными потому что протокол I2C плохо работает на больших расстояниях.
После этого нам нужно очистить код примера MPU9250BasicAHRS от ненужных нам фрагментов. Например, можно удалить фрагменты кода, отвечающие за работу с ЖК дисплеем. Также в код примера мы добавим фрагмент кода для авто калибровки кода. Модифицированный таким образом код можно скачать по следующей ссылке.
После этого загрузите данный код программы в вашу плату Arduino. Откройте окно монитора последовательной связи, измените скорость на 115200, вы должны увидеть следующее:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
MPU9250 9-DOF 16-bit motion sensor 60 ug LSB MPU9250 I AM 71 I should be 71 MPU9250 is online… x-axis self test: acceleration trim within : 0.8% of factory value y-axis self test: acceleration trim within : -1.9% of factory value z-axis self test: acceleration trim within : 1.8% of factory value x-axis self test: gyration trim within : -0.2% of factory value y-axis self test: gyration trim within : 0.3% of factory value z-axis self test: gyration trim within : 0.6% of factory value MPU9250 bias x y z 254913-660mg1.1-0.11.2o/s MPU9250 initialized for active data mode…. AK8963 I AM 48 I should be 48 AK8963 initialized for active data mode…. Mag Calibration: Wave device in a figure eight until done! |
Если вы видите:
|
1 2 3 4 5 6 |
MPU9250 9-DOF 16-bit motion sensor 60 ug LSB MPU9250 I AM FF I should be 71 Could not connect to MPU9250: 0xFF |
То это будет означать проблемы с подключением датчика. В худшем случае это может быть неисправность платы Arduino или датчика. Устраните эти проблемы прежде чем продолжать.
Если все идет хорошо и вы видите сообщения “MPU is online” и “Mag Calibration: Wave device in a figure eight until done!”, то вы должны начать перемещать ваш датчик MPU9250 по фигуре восьмерки (цифра “8”) до тех пор пока датчик не закончит автоматическую калибровку. После этого вы должны увидеть значения параметров yaw, pitch и roll:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
Mag Calibration: Wave device in a figure eight until done! Mag Calibration done! X-Axis sensitivity adjustment value 1.19 Y-Axis sensitivity adjustment value 1.19 Z-Axis sensitivity adjustment value 1.15 AK8963 ASAX 1.19 ASAY 1.19 ASAZ 1.15 Yaw, Pitch, Roll: 11.34, 28.62, 50.03 Yaw, Pitch, Roll: 20.47, 25.15, 52.88 Yaw, Pitch, Roll: 26.94, 19.02, 52.70 Yaw, Pitch, Roll: 28.22, 15.02, 50.15 Yaw, Pitch, Roll: 27.10, 13.94, 44.68 Yaw, Pitch, Roll: 23.11, 13.69, 37.51 Yaw, Pitch, Roll: 14.29, 13.22, 27.61 Yaw, Pitch, Roll: 357.03, 8.21, 16.72 Yaw, Pitch, Roll: 342.29, 0.69, 9.19 Yaw, Pitch, Roll: 328.42, -4.80, 3.16 Yaw, Pitch, Roll: 317.19, -10.51, -0.58 Yaw, Pitch, Roll: 311.88, -16.57, -3.64 Yaw, Pitch, Roll: 327.71, -23.45, -16.82 Yaw, Pitch, Roll: 325.74, -22.02, -23.51 Yaw, Pitch, Roll: 325.99, -28.17, -26.95 Yaw, Pitch, Roll: 324.57, -24.96, -23.21 Yaw, Pitch, Roll: 320.01, -26.42, -22.25 Yaw, Pitch, Roll: 322.50, -26.04, -26.62 Yaw, Pitch, Roll: 322.85, -23.43, -29.17 Yaw, Pitch, Roll: 323.46, -19.20, -31.48 |
Автоматическая калибровка азимута (Yaw) RTPT с помощью P-контроллера
Сначала нам необходимо преобразовать значение параметра yaw из диапазона (-180 to +180) в диапазон (0 to 360) с помощью следующей простой формулы:
yaw = yaw + 180;
Затем нам необходимо найти ошибку в параметре yaw используя простой пропорциональный регулятор (Proportional controller), затем прибавить значение этой ошибки к значению параметра yaw. После этого можно будет работать с этим новым значением параметра yaw.
Исходный код программы
Его можно скачать по следующей ссылке.